One of the main purposes of scientific research is to structure the world around us, discovering patterns that transcend and that consequently help to unify applications in various contexts.
In this occasion I would like to show a generic model that has many practical applications, as varied as design of excavation operations, strategies to eliminate military objectives, and selection of projects in companies to obtain greater profits.
A specific case could be the following: frequently most companies have to face equilibrium actions on the realization of certain projects that produce profits and the necessary expenses for carrying out support activities for these projects. Let us suppose that a telecommunications company is evaluating the pros and cons of a project to offer some type of high-speed access service to its customers in the home. The market research shows that this service would produce a good amount of profits, but that they have to be weighed against the cost of carrying out some preliminary projects necessary to make the service possible, for example, increase the fiber optic capacity in the core of the network and the purchase of a new generation of high-speed routers.
What makes these kinds of complicated decisions is that they interact in complex ways: in isolation, the high-speed service gain may not be enough to justify the modernization of the routers; However, once the company has modernized the routers it may be in a position to offer another lucrative project to offer to its customers, and perhaps this new project will tilt the profits in favor of the company. In addition, these interactions can be concatenated: the new project may require other expenses but this may lead to the possibility of other lucrative projects.
In the end, the question would be which projects to devote to and which ones to ignore? It is a simple matter of balancing the costs of realization with the profit opportunities that would be possible.
One way to model these types of decisions is as follows:
There is an underlying set of projects, where each project
has an associated income
which can be positive or negative. Some projects are prerequisite for the realization of other projects. It may be that a project has more than one prerequisite or possibly none. In addition, a project can be a prerequisite for multiple projects. We will say that a set of
projects is feasible if the prerequisites of any project in
are also in the set. A problem to solve would be to find a feasible set of projects with the highest income.
In terms of graph theory we could define this set with the name of closure: A closure in a directed graph is a subset of vertices without output arcs, that is, a subset
such that if
and
then
.
If we assign a weight (of arbitrary sign) to each node
of
, the problem that concerns us is: find a closure
with the greatest possible weight.
In general, our mission would be to partition the set of vertices into two sets and
, the set closure and its complement. The way in which we will model this problem will be a minimum cut in a certain graph. But in which graph? And how to transform negative weights into positive capabilities for the flow algorithm?
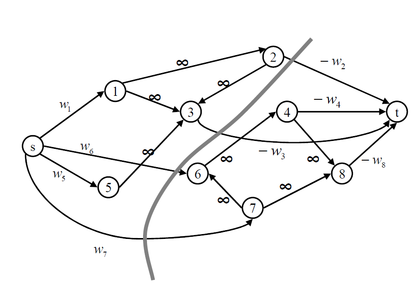
To solve these questions we begin by defining a new graph , formed by adding a source
and a sink
to
. For every vertex
with
let’s add an arc
with capacity
, and in the same way for every vertex
with
let’s add an arc
with capacity
. We will define the capabilities of the arcs in
later. We can see that the capacity of the cut
is
, so the value of the maximum flow is at most
.
We would like to guarantee that if is a minimum cut in this graph, then
is a closure. The way we will achieve this is by defining the capacity of each arc in
as
. Then we can formally define the network in question as:
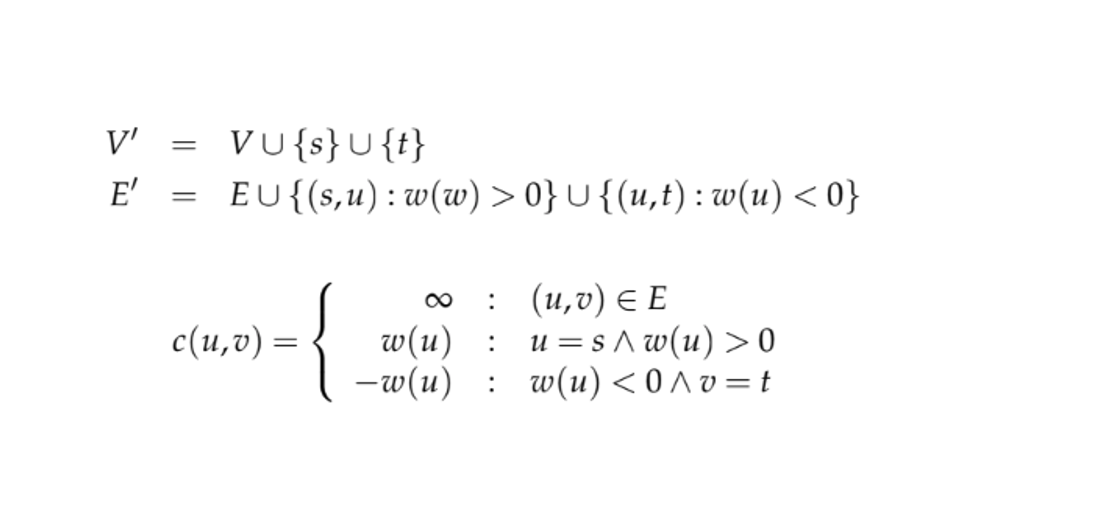Surprisingly, it is possible to demonstrate that there is a bijection between the minimum cuts in this graph and the closures in . So it would only be necessary to know an algorithm to find minimum cuts in a graph to solve the problem that concerns us.
This example is one of the most unexpected applications of the theory of flows that occur in daily life and one of my favorites, which shows us how often we can find mathematical models in the most unexpected places. I hope that this small example have been interesting for all of you. Continue following our blog.
About the author:
José Carlos Gutiérrez Pérez from Cuba is an early-stage researcher (ESR4) within the ROMSOC project. 
He is working at the University of Bremen (Germany) in collaboration with the industrial partner SagivTech (Israel) on the development of new concepts for data-driven approaches, based on neural networks and deep learning, for model adaptions under efficiency constraints with applications in Magnetic particle imaging (MPI) technology.