Even though STEM fields have a reputation of dealing with hard problems that are complicated to understand for someone not working in the field, there are lots of examples, where an unsolved problem is simple enough to be explained at middle school level, for example moving sofa problem, or famous Fermat’s conjecture, that was solved only recently, after being open for centuries. Looking at them, one might ask, how simple can a hard problem be? Can it be so simple, that even child in kindergarten can understand? What about so simple, that even kindergartener can come up with? Most kids like shiny objects. So imagine little girl, about 5, playing in room with several rotating mirrors, marbles and so on. It will not take a while until she starts playing with reflections, either using sun, if the room is bright, or maybe a flash-light if there is one. At first she is playing by reflecting light trough several mirrors, maybe making a vampire face as well, if the room is dark enough, then she moves on marbles and their light on the wall. She will soon start detecting how changing the direction of the flash-light, or changing a position of marbles and mirrors changes light on the wall. And if she will not be disturbed, she will ultimately come up with a question, on which many scientists have spent lot’s of time, on which many PhD theses were written and answer of which worth millions for big companies, but is still an open problem in most cases:
“How should I arrange those things, to get exactly the shape of light I want on the wall?”
One might wonder, what makes this question so hard to answer. After all, reflection rules are taught in middle school physics, why is it hard to to figure out the shape on which this rule should be applied to? In fact, there are simple abstract models, where equations for a mirror are derived from those rules, but those models are quite far from most applications, and even then, having equation does not guarantee to have a good way of solving it. For example, two simplest and relatively well studied models are “Collimated source” and “Point-source”. The Collimated source model assumes that all light rays are parallel and hit the mirror from the same direction (it tries to mimic sun light, but disregards all the refraction happening in atmosphere, so in practice it is good only for some high-tech lasers).
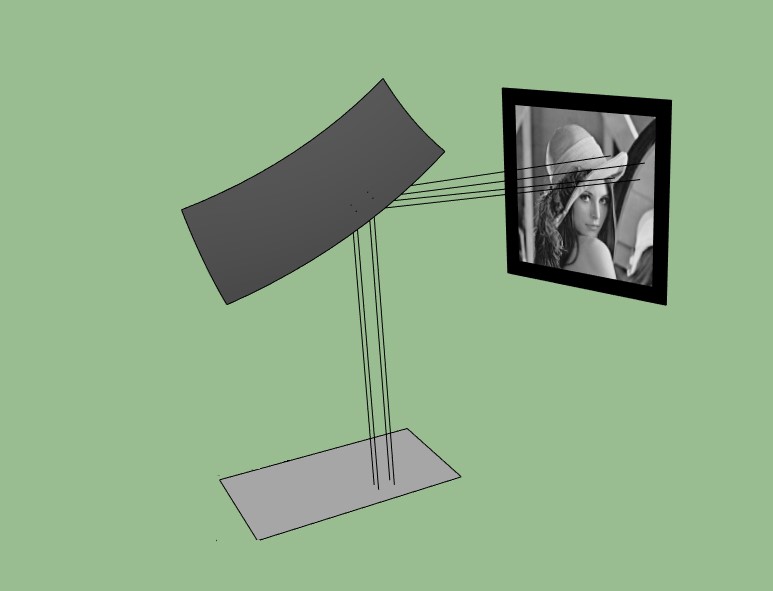
The Point-source model assumes that all light comes from same point (it is a bit closer to realsituations, think about a flash-light, but with really, really small lightbulb).

In those models, a shape of the reflector can be computed from solution of following partial differential equation:
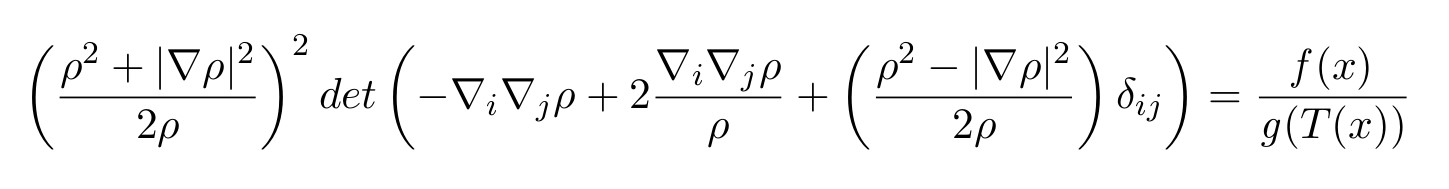
As most mathematical equations, this one looks scary for someone who does not understand what it means, but it is a rare exception in the sense that this equation looks even scarier for those who understand: It is a fully non-linear Monge-Ampere type partial differential equation. For those who don’t know: it means that all classical ways of solving PDEs fail miserably for this one.
Here for the rescue comes Optimal Transport, the theory that originated from the problem which is again very simple to explain, but hard enough, that it has been around for more than two centuries without much progress. Until a couple of decades ago, when it found it’s second breathe and developed into one of the fastest growing mathematical fields: Given an initial distribution of resources, for example bakeries in Paris which produce some amount of fresh croissants every morning, a desired allocation of those resources, for example cafeterias which need some amount of croissants every morning, and a known cost of transporting those croissants from each bakery to each cafeteria, what is the optimal arrangement of transporting those resources, with respect to the total cost, or in other words, how to decide which cafeterias should each bakery supply, in order to minimize the total cost of transporting all
croissants.
This theory has found its way through both fundamental and applied mathematics, physics, natural sciences, economics and technology, providing new developments as well as refreshed views on existing subjects. For above-mentioned optics problems, it provided a new description of same models, which gave them access to all the fruits of Optimal Transport theory, including robust tools for finding solutions.
But even then, there are still lots of simple questions in that small part of optics, that are left open even after using Optimal Transport. For example, what if the light source is not a point, but something bigger? What if there is more then one mirror? So maybe, we should also be asking: How hard can a simple problem be?
About the author:
Giorgi Rukhaia is an early-stage researcher (ESR3) in the ROMSOC project. He is affiliated with the Institut national de recherche en informatique et en automatique (INRIA) in Paris, France and working in collaboration with Signify (former Philips Lighting), the Netherlands. In his research project he is working on an Optimal Transportation computational approach and the development of numerical algorithms for the inverse free-form optical surfaces design using extended sources.