In my last blog post , we got an overview on the origins of sound while highlighting the motivations for the ESR02 subproject within ROMSOC. (TLDR : Its to develop coupled mathematical models to compute the influence of turbulent fluid and porous media on a sound measurements). This time around we focus on simplifying the scope and complexities accounted in a target mathematical model for sound measurements. Measuring sound provides valuable insights in engineering tasks. The knowledge of acoustic characteristics of materials and structures obtained apriori is valuable to designers and architects. Measurements are also necessary to enhance user experience in loudspeakers etc. In product maintenance and diagnostics, e.g of a vehicle, sound signal provides information on health and performance, and is constantly monitored. But how are these measurements performed? Typically, a simplified measurement procedure involves, a receiver, (or sensor) which captures the sound signal. Receivers come with different accuracy, sensitivity and range in sound level measurements. It is also packaged differently to suit the environment. Knowing the measurement environment is extremely important, since enclosures cause reflections of incident sound signals and also induce it’s own resonance. External noise may also deter accuracy and in some cases, there also are chambers designed specifically to prevent external noise from impacting measurements (anechoic chambers). Information about sound source is also to be taken into account. A distribution of sources, e.g a set of loudspeakers can have interference patterns, while a moving source (relative to the receiver) exhibits a shift in frequencies, known as the Doppler effect.

Recreating such an entire procedure on a computer involves replicating the entire setupdigitally – making it necessary to encode the physical process into mathematical equations. The French mathematician, Jean D’Alembert (1717-1783) is credited with arriving at the concise equation describing the motion of a sound wave (in 1D) through a medium,
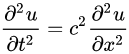
The wave equation is a well-known partial differential equation and is of great importance in various applications. The equation has multiple solutions most of which maybe physically unfeasible and need additional information from the domain of interest to completely describe the motion of sound. This is where models for sound sources and environmental conditions are factored. The image below illustrates the generation of a spherical wave from a point-sized source at the center of the rectangular domain.
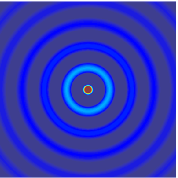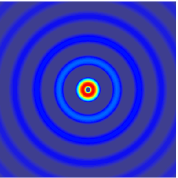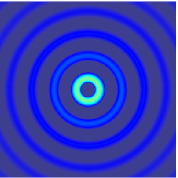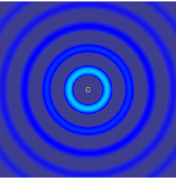
While the wave propagation model above explains the sound propagation in sparsemedium like air, it is complex in porous layer media. Models on acoustical behavior in porous materials were presented only in the 1950s by Zwikker, Kosten and Biot followed until the present by more detailed models. Sound transmission through porous materials are distorted severely influenced by the porous micro-structures and the fractional volume of the air. It is being subjected to viscous and thermal resistances, while also being deferentially transmitted through the fluid within the media and the porous frame. A detailed acoustical model replicating their effects need to consider the macroscopic effects on an incident signal and the choice of the right model depends on the type of porous material in a specific application.
Physical processes in the nature are often observed as a multitude of phenomena happening simultaneously and need simplification to quantify, analyze and predict them. A variety of models need to be sewn together to reproduce the phenomena in a computer accurately. The ROMSOC project aims to address this very issue through mathematical modeling and coupling. Follow our project blog for more posts in the topic.
About the author: 
Ashwin Nayak is an early-stage researcher (ESR2) in the Reduced Order Modeling Simulation Optimization and Coupled methods (ROMSOC) project. He is affiliated with the Technological Institute of Industrial Mathematics (ITMATI), Spain and working in collaboration with Microflown Technologies B.V., Netherlands. His research aims to develop coupled mathematical models to enable acoustical measurements in fluidporous
media interactions.

One Reply to “Mathematical modelling acoustic measurements”
Comments are closed.