There I was considering my options after graduation. Different thoughts were rambling across my mind, the idea of getting an advanced degree like Ph.D., and learning a topic at a deeper level intrigued me. I truly enjoyed working on my master thesis and decided to pursue my Ph.D. in the same field.
So, what do I do? Ah, the question that triggers an existential crisis. Sometimes, this comes from innocent, friendly strangers who are trying to spark a conversation. This image from the ‘PhDcomics’ really justifies the length of time it takes you to answer the question “So, what do you do?” Hmm… Let me try to explain it. Just hang in there, you are bound to understand one of the modern problems in the financial mathematics and my humble efforts to solve it.
Problem:
Packaged retail investment and insurance products (PRIIPs) are at the essence of the retail investment market. PRIIPs offer considerable benefits for retail investors which make up a market in Europe worth up to € 10 trillion. However, the product information provided by financial institutions to investors can be overly complicated and contains confusing legalese. To overcome these shortcomings, the EU has introduced new regulations on PRIIPs (European Parliament Regulation (EU) No 1286/2014). According to this regulation, a PRIIP manufacturer must provide a key information document (KID) for an underlying product that is easy to read and understand. The PRIIPs include the interest rate derivatives such as floating coupon bonds, or interest rates cap and floors.
A KID includes a section about ‘what could an investor get in return?’ for the invested product’ which requires costly numerical simulations of financial instruments. Generally, the interest rate derivatives are evaluated based on the dynamics of the short-rate models. For the simulations of short-rate models, techniques based on discretized convection-diffusion reaction partial differential equations (PDEs) are often superior. It is necessary to note that the choice of a short rate model depends on the type of financial instrument. The Hull-White model is one of the examples of the short rate models:
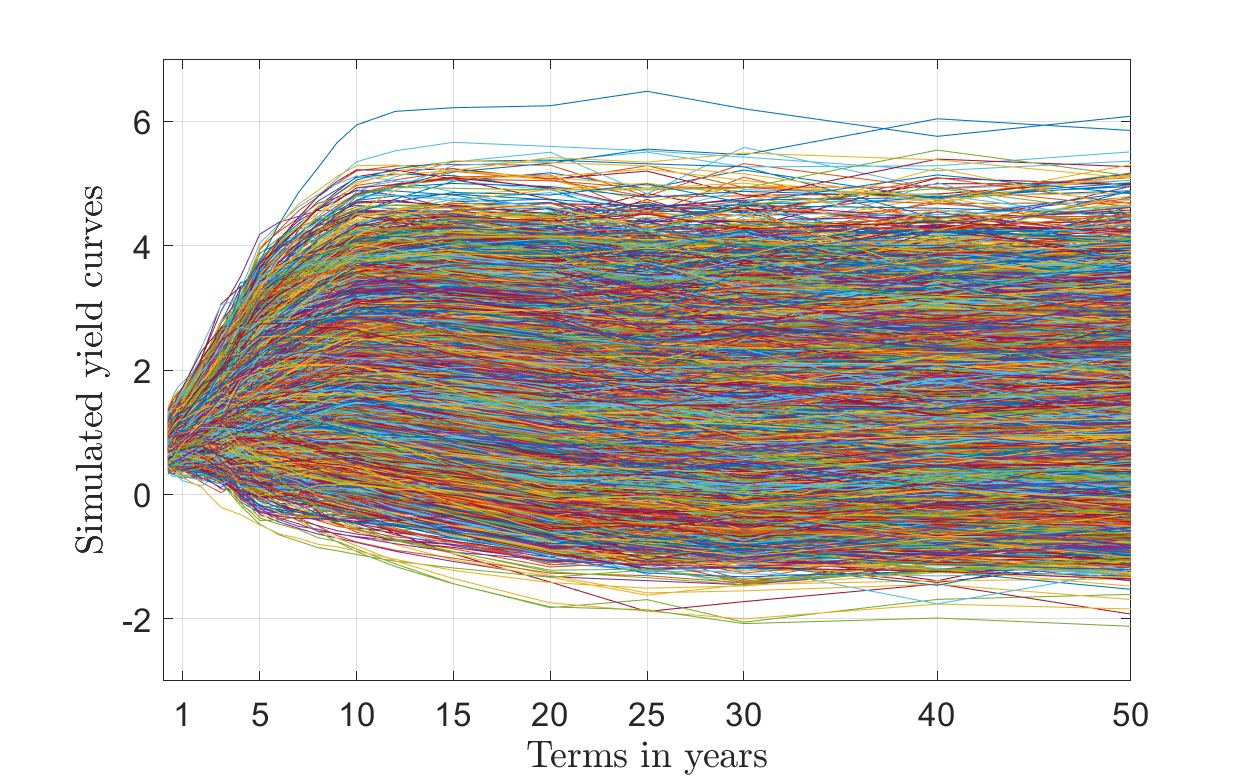
The model parameters are usually calibrated based on market structures like yield curves. A yield curve shows the interest rates varying with respect to the 20-30 time points known as ‘Tenor points’.
Current idea:
So, in short, the goal is to reduce the computational complexity in the analysis of financial instruments. To avoid this problem, we are working on a parametric model order reduction (MOR) approach based on the proper orthogonal decomposition (POD) method. The method is also known as the Karhunen-Loève decomposition or principal component analysis in statistics. This research work aims to develop a MOR methodology regardless of any short rate model. The technique of model order reduction reduces not only the computational complexity but also the computational time. POD generates an optimally ordered orthonormal basis in the least squares sense for a given set of computational data. Further, the reduced order models are obtained by projecting a high dimensional system onto a low dimensional subspace obtained by truncating the optimal basis. The selection of the computational data set plays an important role, and most prominently obtained by the method of snapshots. In this method, the optimal basis is computed based on the set of state solutions. These state solutions are known as snapshots and are calculated by solving the full model obtained by discretizing the PDE for some parameter values.
The calibration based on simulated yield curves leads to the size of parameter space. Each parameter vector
has values ranging from
to
, where
is the total number of tenor points and
. We compute the snapshot matrix for some selected values of parameters (i.e., snapshots taken at some nodes
).
The process of computing the optimal basis independent of such a high dimensional parameter space is complex. We aim to develop a new algorithm to obtain the optimal basis based on tensor numerics. We construct a snapshot tensor comprises of the snapshot matrices obtained for certain parameter vectors. Furthermore, we factorize the snapshot tensor using the tensor decomposition techniques to generate the optimal basis. We will then use this optimal subspace for obtaining a parameter-independent reduced order model.
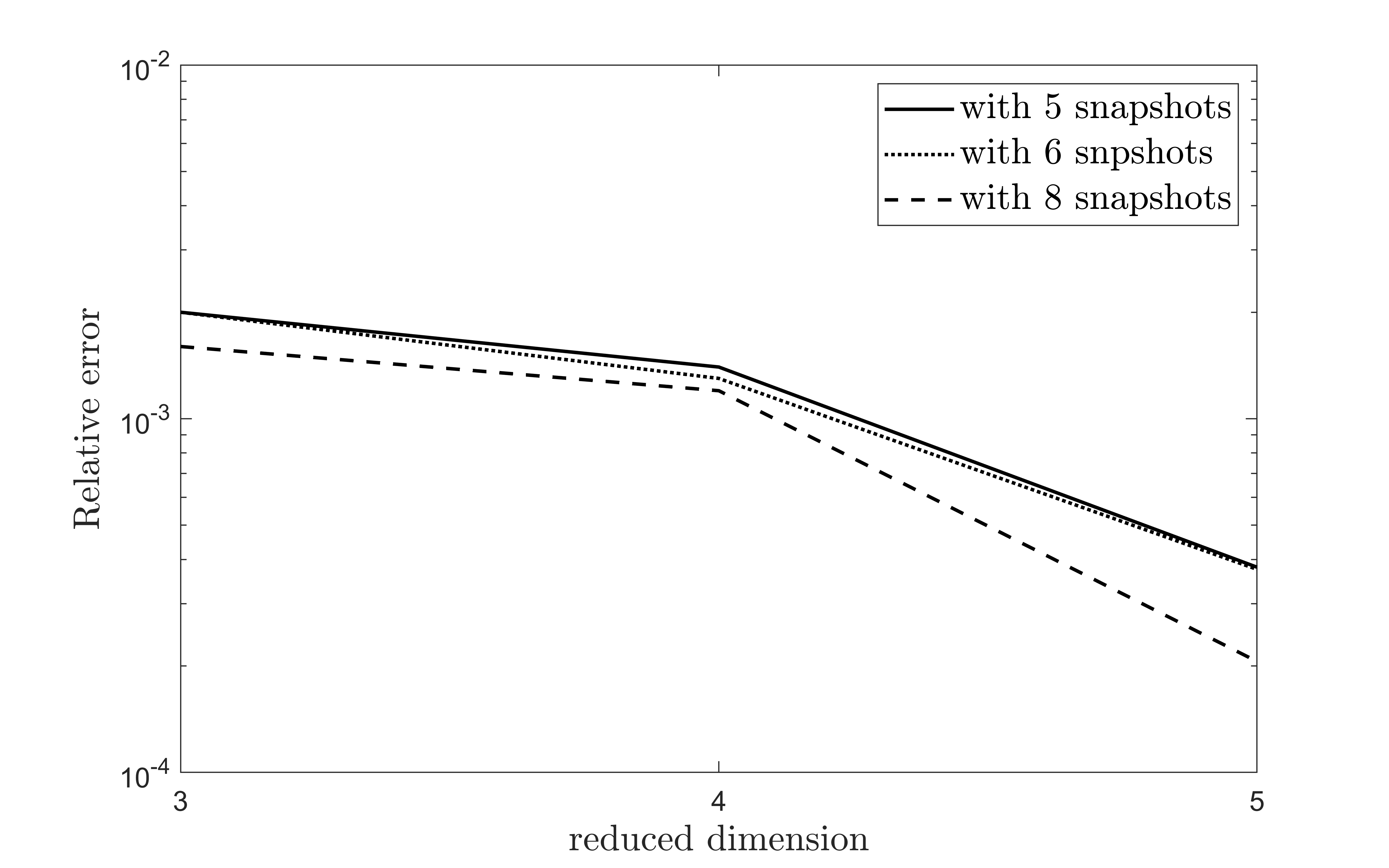
We have implemented the classical POD approach for a numerical example of a puttable bond solved using a Hull-White model. The current research findings indicate that the MOR approach works well for the short rate models and provides two to three times computational speedup (see Fig. 2).
About the author:

Onkar Sandip Jadhav is an early-stage researcher (ESR6) in the ROMSOC project. He is a PhD student at the Technische Universität Berlin (Germany) and is working in collaboration with MathConsult GmbH (Austria). In his research he is working on a parametric model order reduction (MOR) approach aiming to develop a new MOR methodology for high-dimensional convection-diffusion reaction PDEs arising in computational finance with the goal to reduce the computational complexity in the analysis of financial instruments.